Karnaugh Maps: A Visual Approach To Boolean Logic Simplification

Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Related Articles: Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Introduction

With great pleasure, we will explore the intriguing topic related to Karnaugh Maps: A Visual Approach to Boolean Logic Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Karnaugh maps, often referred to as K-maps, are a powerful tool used in digital logic design to simplify Boolean expressions. This simplification process is crucial for minimizing the number of logic gates required to implement a circuit, leading to smaller, faster, and more efficient designs.

Understanding the Basics

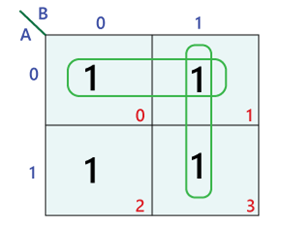
At its core, a Karnaugh map is a graphical representation of a truth table. It visually organizes the possible input combinations and their corresponding outputs, enabling the identification of patterns and redundancies that simplify the Boolean expression.

Each cell in the K-map corresponds to a unique combination of input variables. The arrangement of cells follows a specific pattern, ensuring adjacent cells differ by only one input variable. This arrangement allows for the easy identification of groups of adjacent cells with the same output value.

Constructing a Karnaugh Map

The construction of a K-map involves the following steps:

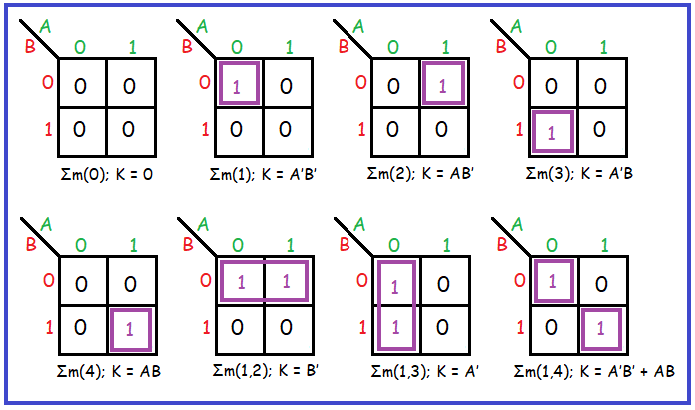
1. Determine the number of input variables: The size of the K-map depends on the number of input variables. A 2-variable K-map has four cells, a 3-variable K-map has eight cells, and so on. The general formula for the number of cells is 2^n, where n is the number of input variables.

2. Label the rows and columns: Each row and column represents a unique combination of input variables. The labeling follows a Gray code pattern, where only one bit changes between adjacent rows or columns. This ensures that adjacent cells differ by only one input variable.

3. Populate the cells: For each input combination, determine the corresponding output value from the truth table and enter it into the appropriate cell.

Simplifying Boolean Expressions

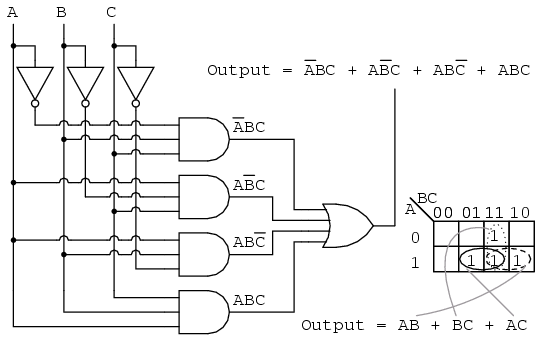
The key to simplifying Boolean expressions using K-maps lies in identifying groups of adjacent cells with the same output value. These groups are called implicants. The larger the group, the simpler the corresponding Boolean term.

Rules for Grouping Cells:

1. Adjacency: Cells are considered adjacent if they share a common edge, even if they are on opposite sides of the map.

2. Size: Groups can be any size, as long as they are a power of two (1, 2, 4, 8, etc.).

3. Maximization: Aim to form the largest possible groups while adhering to the previous rules.

4. Overlapping: Groups can overlap, but each cell should be included in only one group.

Once the groups are identified, the corresponding Boolean terms are determined. Each group represents a product term, where the variables included in the group are ANDed together. The final Boolean expression is the sum of all the product terms.

Benefits of Using Karnaugh Maps

1. Visual Simplification: K-maps provide a clear and intuitive visual representation of the Boolean expression, making it easier to identify patterns and redundancies.

2. Reduced Logic Gates: By simplifying the Boolean expression, the number of logic gates required to implement the circuit can be significantly reduced.

3. Improved Performance: Fewer logic gates lead to faster signal propagation and lower power consumption.

4. Enhanced Design: K-maps facilitate a more systematic and efficient design process, reducing errors and improving circuit reliability.

Frequently Asked Questions (FAQs) about Karnaugh Maps

1. What is the maximum number of input variables that can be handled by a Karnaugh map?

There is no theoretical limit to the number of input variables that can be handled by a K-map. However, for practical purposes, K-maps become increasingly complex and difficult to use as the number of variables increases. For more than five input variables, alternative methods like Quine-McCluskey algorithm are generally preferred.

2. How do I handle "don’t care" conditions in a Karnaugh map?

"Don’t care" conditions occur when the output value is irrelevant for certain input combinations. These conditions can be represented by an "X" in the corresponding cells on the K-map. When forming groups, "don’t care" conditions can be included to form larger groups and simplify the expression further.

3. Can I use a Karnaugh map for more complex Boolean expressions?

While K-maps are particularly useful for simplifying expressions with up to four or five input variables, they can be applied to more complex expressions by using a multi-level approach. This involves breaking down the complex expression into smaller sub-expressions, simplifying each sub-expression using K-maps, and then combining the simplified sub-expressions to obtain the final simplified expression.

4. What are some alternative methods for simplifying Boolean expressions?

Besides Karnaugh maps, other methods for simplifying Boolean expressions include:

• Quine-McCluskey Algorithm: This is a more systematic and algorithmic approach that can handle expressions with a larger number of input variables.
• Espresso Algorithm: This is a more sophisticated algorithm that utilizes a combination of Boolean algebra and heuristic techniques for optimal simplification.

Tips for Using Karnaugh Maps Effectively

1. Start with a clear truth table: Ensure the truth table accurately represents the desired logic function.

2. Label rows and columns carefully: Use the Gray code pattern to ensure adjacent cells differ by only one input variable.

3. Identify the largest possible groups: Aim to form the largest groups to minimize the number of product terms.

4. Use "don’t care" conditions strategically: Include "don’t care" conditions to form larger groups and simplify the expression further.

5. Verify the simplified expression: After simplifying the expression using the K-map, verify the result by comparing it to the original truth table.

Conclusion

Karnaugh maps are a powerful and intuitive tool for simplifying Boolean expressions, a fundamental task in digital logic design. They offer a visual representation of the logic function, enabling efficient identification of patterns and redundancies that lead to simplified expressions. This simplification results in reduced logic gate count, improved circuit performance, and enhanced design efficiency. While K-maps are particularly effective for expressions with up to five input variables, they can be used for more complex expressions with a multi-level approach. Understanding and effectively utilizing Karnaugh maps is crucial for any aspiring digital logic designer.

Closure

Thus, we hope this article has provided valuable insights into Karnaugh Maps: A Visual Approach to Boolean Logic Simplification. We thank you for taking the time to read this article. See you in our next article!